Introduction

The general outline of this story is to start off by putting you “in touch” with the state of physics at the beginning of 1895. Physicists were feeling pretty confident that they understood most everything. Sure there were a few loose ends, but they were just loose ends.

1895 marks the year when people began tugging at the loose ends and things unraveled a bit. In the next 3 years, three major discoveries made it plain there was still a lot to learn at the fundamental level.

Once I’m there I will concentrate on a very, very small object… that ties in with stars, arguably the biggest objects there are (galaxies are basically collections of stars). And we would never have seen this but for those discoveries in the 1890s.

It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.

And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it… but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)

Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I used 9.8 kg m/s² last time for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.

A Couple of Go Backs

Remembering my previous post on mass, one might wonder, “why bother with this sort of thing? Why should people investigate such things?”

We live in an orderly universe. This is a good thing. It gives us confidence that when we set the groceries on the counter, they won’t jump up and bite us. (Not even Darwin’s live food groceries.) It also means that when we drop a car battery on our feet, we know it!

The point of science, when it is being properly done, is to increase our understanding of this world we are in.

All that work on forces and masses and weight was at its core an exercise in breaking down phenomena we see every day into different effects and studying one of them. We removed friction and gravity from the picture and analyzed what was left. Then we took up gravity. What we didn’t get to was showing that friction is itself a force.

With that kind of understanding, you can predict what will happen in an environment where gravity is different, e.g., on the moon and in orbit. At first you won’t be used to it, but then you do get used to it. There are plenty of stories of astronauts who adapt so well to “microgravity” (i.e., the lack of any sort of sensation of “down”) and free fall that they will come home, put the toothpaste on the toothbrush, and drop the toothpaste tube, because they’re used to just letting it go and having it stay there until they’re ready to put things away. They’re applying Newton’s first law (objects at rest will stay at rest) since it is pretty much unmodified in orbit, no need to worry about gravity pulling things to the floor.

Another Go Back. Last time I rather casually used the concept of acceleration, without really going into it much. I assumed some knowledge that many might not have.

You can think of acceleration as change in speed, the faster the change, the greater the acceleration. And it can be a decrease as well as an increase; to a physicist it’s still an acceleration, albeit one which is in the reverse direction to the motion.

I know, too, I said things like “meters per second per second” a lot. That wasn’t a stammer. That’s truly how you measure acceleration. Think about a sports car, able to go from zero to 60 miles an hour in four seconds. That means, on average, every second of that four seconds, the car’s speed increases by 15 miles per hour. So it accelerates at 15 miles per hour every second, which is to say at 15 miles per hour per second. That can even be written as 15 miles / hour / second (the “per” functioning as a division). Or even, 15 miles • 1/hour • 1/sec.

Yes, when physicists do math, they will multiply and divide by units, not just the numbers. They can be divided and multiplied, and even follow the rules of cancelation. (Chemists often have to convert from one unit to another, like calories to Joules, so they really do this sort of thing a lot.)

Notice there are two time units (hours and seconds) in the denominator. It’s kind of funny that they don’t match. You could convert the hours into seconds, like this: Use the fact that there are 3600 seconds in an hour and do the following: 15 miles • 1/hour • 1/sec • 1 hour/3600 sec.

That last term is simply 1 hour divided by 3600 seconds, which is 1. You can multiply by 1 without changing anything. But now that it’s there, the 2 hours, one in the numerator and the other in the denominator, cancel.

Do that cancellation and you have 15 miles • 1/hour • 1/sec • 1 hour/3600sec, and you can re-arrange to get 15/3600 • miles/sec/sec or 1/240 miles per second per second or 0.004167 miles / sec². You could then move on to convert miles to meters (1609 meters is one mile, roughly), and that works out to be 6.7 m/s², and it turns out that car is accelerating about 2/3 as much as gravity accelerates a falling object.

You may have noticed I seem to prefer metric, and that’s because just about every bit of my technical education was in metric; I’m used to it. When I got exposed to the occasional rocketry done in pounds force and pounds mass, it was like trying to use stone knives and bearskins (and you needed to know when you had to multiply or divide by that 32). Obviously it works (we put men on the moon after all), but it just seems cumbersome to me.

(And a note for the fussy, you’ll notice I’ve sometimes spelled out a unit, e.g., “second” and sometimes abbreviate it “sec” or “s.” That last one, just a plain s, is the “official” metric abbreviation for second. Likewise meters, m, and kilograms, kg. But sometimes I spell things out too, as a reminder.)

But the notion of acceleration (however you measure it) depends on speed… actually, it is dependent on velocity.

Velocity

So my second “go back” actually leads us into today’s topics. Let’s flesh out velocity.

Velocity is both how fast something is moving, and in what direction. So it’s actually a more complex concept than the one we talked about last time, mass. The distinction between mass and weight was probably odd to many, but at least mass can be expressed as a number. Velocity? You need a number (your speed), and a direction. (Or maybe you can get by with a bit less… stay with me.)

Direction is easy on a straight highway. You’re either going forward or backward. Since there’s only two choices, and they are opposite of each other, it’s natural to consider the forward direction positive and the backward direction negative. So driving 60 mph in fourth gear is +60 mi/hr, but switching to reverse (after first stopping, since we don’t want your engine to leap through your hood in an ugly mess), and going fairly fast in reverse might get you -10 mi/hr. The local constabulary, using a radar gun, will measure your speed and may—depending on circumstances—pull you over to inform you how fast you were going and how much you will have to pay for that.

You can even add and subtract your velocities, just like you do with masses. The usual example here is a railroad car moving along on tracks, also nice and tidy and one-dimensional. If the train is moving at 60 mi/hr and a pitcher is in a cattle car, playing catch with someone, and he throws the ball forward at 60 mi/hr, someone standing on the side of the tracks will see the ball moving at 120 mi/hr, because the speed of the train and the ball add together. If he and the catcher switch places, he’s now throwing the ball at -60 mi/hr and the ball is now stationary as far as the guy by the side of the tracks is concerned: +60 mi/hr plus -60 mi/hr = zero.

OK, I’ve used a very limited situation to make a couple of points, but it’s not very interesting in the real world. What about two or even three dimensions?

I’m going to do what everyone else does when explaining velocity in two dimensions: I’m going to use a pool table as my example. It’s the best choice I can think of, and I guess that was the best they could come up with too.

Let’s say the pool table points north-south along its length. A ball is moving directly north at 1 m/s. Another ball is moving directly east at 1 m/s. They have the same speed, but different velocities, because the direction of motion is different.

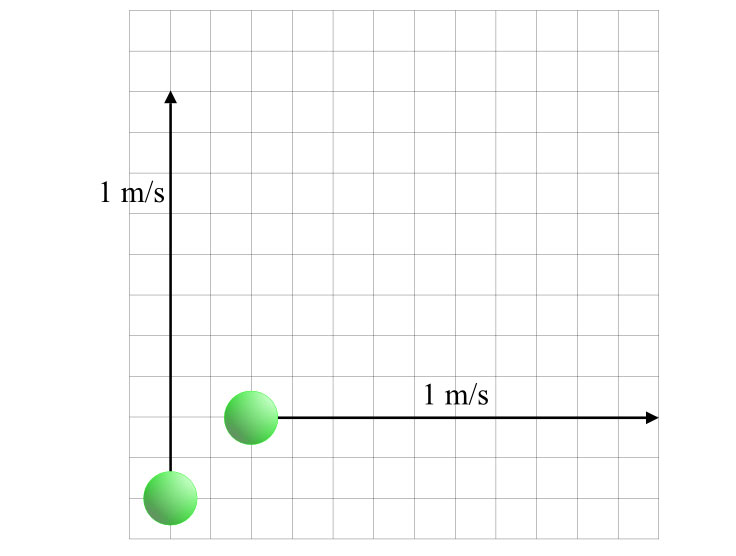Figure 2-1: Two balls moving at one meter per second so they have the same speed, but they are moving in different directions so they have different velocities.

Now let’s consider a different ball, a red one moving at 1 m/s exactly to the northeast. If you think about it, that ball is moving north at a certain rate, and at the same time it’s moving east at a certain rate. Or to put it another way, how fast would a ball (let’s make this one pale blue) moving straight east have to move so that it’s always directly south of the diagonally-moving ball? And how fast would a (purple this time) ball moving straight north have to move so that it’s always directly west of the diagonally-moving ball?

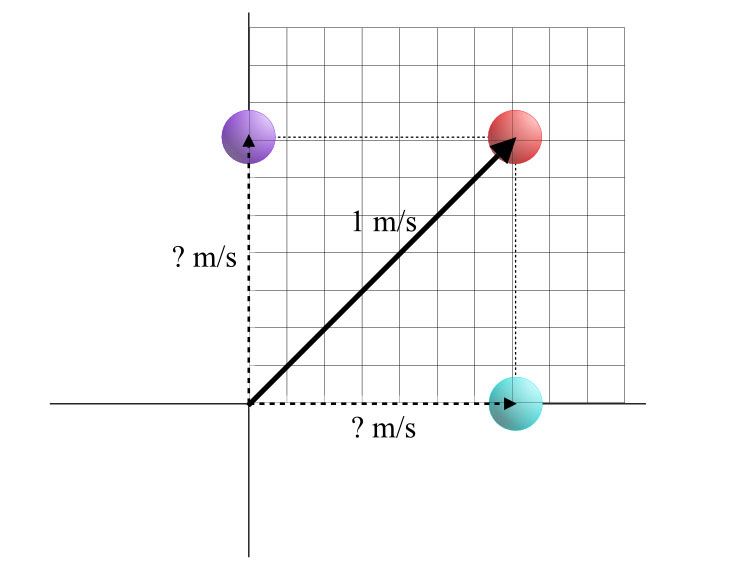Figure 2-2: How fast does the purple ball have to move so it’s always exactly west of the red ball, which is moving diagonally? Similarly, how about the turquoise ball? How fast must it move on the horizontal line to stay exactly south of that red ball?

You can do this visually by drawing a diagram like this, then measuring the vertical and horizontal lines. You should get about .7 the length of the diagonal line. Since that diagonal line is 1 m/s, the horizontal and vertical lines should be .7 m/s. (The exact number is actually 1, divided by the square root of 2. That can be derived from the Pythagorean Theorem. To six places, it’s 0.707107, but you will never be able to measure quite that accurately off a drawing you made on a piece of paper.)

You can do this with any velocity, big or small, in any direction. You can break it down into a north-south component and an east-west component.

So any velocity on the pool table can be expressed with numbers, but by writing two numbers, not one. Our diagonal moving ball has a velocity of [ 0.707 north, 0.707 east ] meters per second.

That pair of numbers is enough to do the job of a speed and a direction.

The Vector

And this is what is called a vector in its mathematical form.

You can also represent a vector by picking a scale (1 inch equals 1 m/sec, for instance), and drawing an arrow with the appropriate length, pointed in the appropriate direction. We’ve already done that. You can’t compute things this way but it sure does help you visualize it. And you can get estimates by measuring off the diagram if you’re careful drawing it.

Vectors are considered equal if they have the same length (mathematicians call this the “magnitude” of the vector) and the same direction. There’s no notion built into a vector of “where it starts” and “where it ends.” We can move them around for convenience, especially on those diagrams, just so long as we don’t stretch them or rotate them.

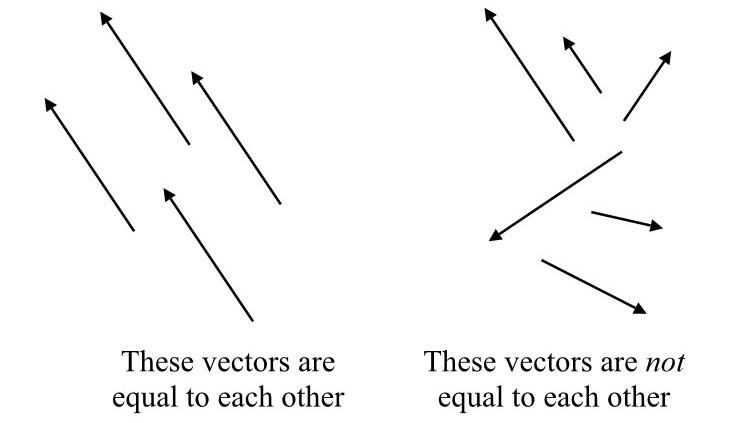Figure 2-3: Vectors are equal to each other if they have the same length and distance, they are not equal to each other if they are of different lengths (“magnitudes”) even if they’re in the same direction, nor are they equal to each other if they have the same magnitude but different directions.

If you think back to last time, I talked about force, mass and acceleration. F = ma. But it turns out the force is a vector. When you push on something, you’re pushing in a certain direction. Likewise, acceleration is a vector too, you’re speeding up in a certain direction. It’s customary to write vectors in bold face (or if on a blackboard, by drawing a line with a little arrowhead over the letter). So it’s actually F = ma.

Mass was not written in bold, because it takes a single number to express it; it doesn’t have direction. (Weight does. Why?) Such plain-old-number quantities are called scalars in distinction to vectors.

Returning to our current topic, velocity is abbreviated v, bold because it’s a vector. So in our diagonally moving ball example, v = [ 0.707 north, 0.707 east ] m/s.

When you take a vector and express it like this, you’ve broken it down into its north and east components. It actually doesn’t matter which two directions you use, so long as they’re perpendicular, but for now let’s stick with north and east.

Even a total distance moved can be a vector. The total distance is equal to the elapsed time, t, times the speed or velocity (depending on whether you want just the distance, or the distance and direction). d = vt.

What happens when you multiply a vector by a scalar, as shown here? What you do on a diagram, is make the arrow that much longer or shorter. Mathematically, you go to each component of the vector and multiply each one by the scalar. In the case of the diagonal moving ball, you have:

d = 5s [0.707, 0.707]m/s = [3.535, 3.535]m.

This is how far the ball has gone, relative to where you first started watching it 5 seconds before. (And it would go right off the pool table, too, if not for the bumpers. More on that later.)

Mathematicians like to do things as generically as possible. So they will write vectors in terms of x and y, rather than north and south. That means they’re not really wedded to any particular orientation. Remember I said it didn’t matter which directions you used, so long as they were at right angles to each other. For convenience when they draw diagrams, the x direction is to the right, and the y direction is upward, the y axis being 90 degrees counterclockwise from the x axis.

You can do more to vectors than just multiply them by a scalar. They can be added together, provided they’re in the same units. (No fair adding speed to force!) This also means they can be subtracted.

Of course when dealing with pure mathematics (as opposed to mathematics applied to physics), generally units are not a concern. Like in the following example.

On a diagram, take your first vector, whatever it is, and then put your second vector so that its tail is right at the head of the first vector. Then draw a new vector from the tail of the first vector to the head of the second vector. That’s the sum of the two vectors. Mathematically, you add each individual element. So:

[ 3, 4 ] + [ -1, 6 ] = [ 3-1, 4+6 ] = [2, 10].

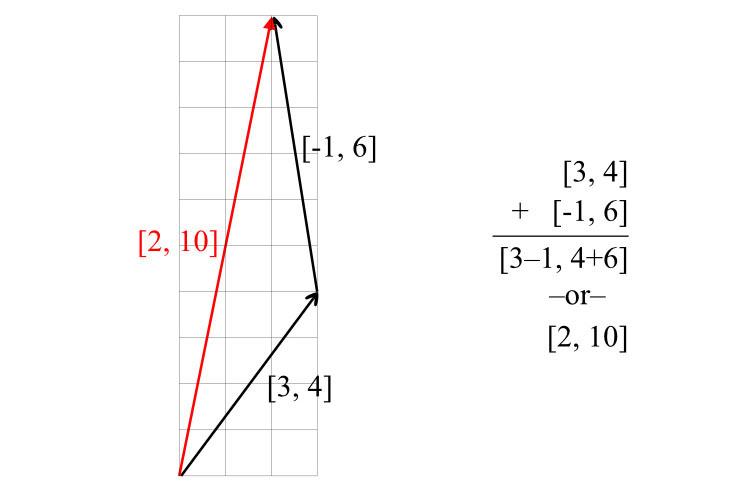Figure 2-4: Vector addition. The two black vectors add up to the red one; vectors must be placed “head to tail” to add them pictorially.

Conservation of Velocity?

So now let’s go back to the pool table, make the scenario slightly more complicated and see what we can use this whiz-bang vector thing to figure out.

This is pool, after all, balls are supposed to hit other balls. So, if we have a cue ball moving along in the x direction at, say, 1 m/s… or more rigorously [ 1.0, 0.0 ] m/s, and it hits another billiard ball head on, what happens? Well, the cue ball hits the other ball. Then the cue ball stops, and the second ball continues on along the x direction, also at 1 meters per second.

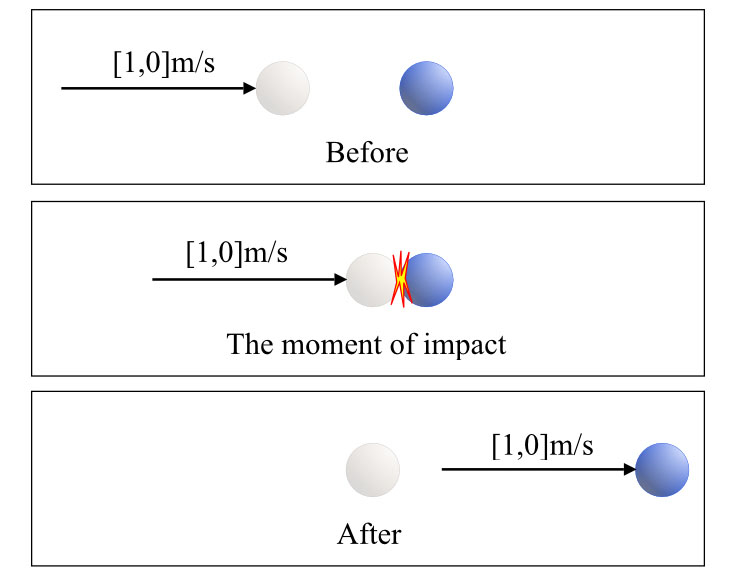
Figure 2-5: Two billiard balls, head-on collision between a moving and a standing ball.

It’s as if the velocity transferred from the cue ball to the other ball, perfectly. So, is it possible we’re on the track of another conservation law, conservation of velocity?

Let’s do a little more investigation. For starters, consider a glancing blow. Let’s have the cue ball moving at 1 m/s in the x direction (ahem) v = [1.0, 0] m/s, and hit the other ball quite a bit off from head on, as shown below.

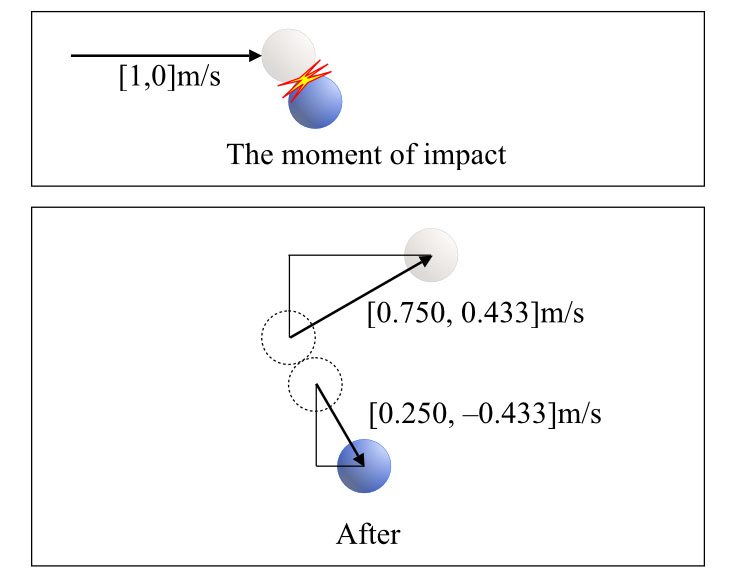
Figure 2-6: Billiard balls, an off-center collision. This time both balls move after the collision.

You’ve seen this happen often enough, you know the cue ball will, in this case, continue moving, up and to the right. And the second ball will move down and to the right. And perhaps one of the two balls moves at a steeper angle than the other. That doesn’t look very much like velocity was conserved, does it? A motion in the x direction turns into two sort-of-diagonal motions?

But actually, when you look at it a bit closer, it looks good. As you can see, we’ve broken the two vectors into their x and y components.

We started with the cue ball moving at [1, 0]m/s, and the other ball (not) moving at [0, 0]m/s. Afterwards, the cue ball is moving at [0.750, 0.433]m/s and the other ball is moving at [0.250, -0.433]m/s.

If velocity is conserved, the sum of the velocities before must equal the sum of the velocities afterwards. These are vectors, and I already told you how to add vectors. So let’s do some addition:

Before: Cue ball [1, 0]m/s + Other ball [0, 0]m/s = [1, 0]m/s.

After: [0.750, 0.433]m/sec + [0.250, -0.433] = [1, 0] m/s.

So it does look like velocity is conserved. Yes, here I could have just made up the numbers to make it work out, but the fact of the matter is in real life, these billiard ball examples really do work out like this.

(And, since I did contrive this scenario, the direction of the cue ball is 30 degrees “up” from the x axis, and its speed is 0.866 m/s. The other ball is moving “down” at a 60 degree angle, at a speed of 0.5 m/s. Those who took some trigonometry might remember there’s something special about 30 and 60 degree angles and the square root of 3, divided by 2.)

A pool player will have played so many games of pool that he knows this behavior in his gut; he knows exactly where to hit the other ball with the cue ball to get the angle he wants, to send that other ball into the corner pocket.

But if it’s a conservation law, it has to hold all of the time, not just in billiards scenarios. And this one doesn’t hold all of the time in billiards, much less in the “real world.”

Nope, No Conservation of Velocity

What happens when a ball hits the bumper? If it hits the bumper head on at 1 m/s, it bounces back at 1 m/s, in the opposite direction. In other words, whatever the vector was before, it’s now a vector in the opposite direction. That’s not conservation!! (And the pool player knows this one too, of course.)

Also, not quite within the realm of billiards, what if the balls are of different weights… er, masses? You already know from your own personal life what will happen. Hit a pool ball with a cannonball and the pool ball will go rocketing away, much faster than the cannonball was moving, and the cannon ball will slow down the tiniest but not stop moving. Reverse the process, hitting the cannonball with the cue ball, and it will barely budge, but the cue ball will bounce back the way it came.

If you want to mess with a pool player, randomize the masses of the balls. Because normally all of the balls have exactly the same mass, at least as close as the manufacturer can make it. In real life very few objects have the same masses. As soon as the masses are different the tidy behavior we illustrated above goes right out the window and the player can’t predict what will happen.

So if you do some experimenting, it seems like what might be getting conserved is not velocity, but something that is the product of mass times velocity. You have to add the mass times velocity, before and after, and that will be conserved. A heavy object will move less under the same impetus from some other object, than a light one would. If mass goes up, velocity goes down to compensate, and vice versa.

Momentum

That product of mass times velocity is known as momentum. And it’s a scalar times a vector, so it’s a vector, too. And for some reason, they chose to symbolize it with p. (They didn’t use m because m is mass, but why did they pick p instead of q or u or… ?). p = mv. And if m is in kilograms, and velocity is in meters per second, we can define the momentum as being in kilogram meters per second, kg•m/sec. That way we can avoid the use of a fudge factor, since the units are already consistent with each other. There is, unfortunately, no named unit of momentum like there is with force (the Newton), so “kilogram meter per second” it is.

OK, that takes care of the unequal masses behaving oddly, but what about a ball rebounding off one of the bumpers?

Actually, what’s happening there is that the ball is striking a much more massive object—the pool table. And the pool table is firmly fixed to the entire planet, if nothing else by friction.

So the entire Earth, it turns out, is reacting to that ball hitting the bumper, and picking up motion in that direction, but the earth is so massive that the motion is very, very small. In fact, in order to make the ball rebound, the momentum of the ball is changing by twice its prior value. If the mass of the ball is b, and it was moving at 1 m/s in the x direction before, its momentum was [ b, 0 ]kg•m/s before, and afterwards its moving in the opposite direction with a momentum of [ -b, 0 ]kg•m/s. Net change in momentum is [ -2b, 0 ]kg•m/s. The earth has to make up this change by gaining [ 2b, 0] kg•m/s. But the earth’s mass is much, much, much more than b, so the velocity imparted by the ball to the earth is microscopic. If one goes up the other has to come down to compensate.

One could complain that since we can’t measure the earth’s “rebound” in this case, maybe it isn’t rebounding. But the absence of evidence (i.e., the failure to be able to measure it) isn’t the same as the evidence of absence (i.e., evidence the earth doesn’t actually rebound when the ball hits the bumper). If we had a way of measuring the earth’s rebound that was sensitive enough to show what we expect based on theory, and it didn’t show that change, then we’d have evidence that momentum isn’t conserved. But if we know our measuring is inaccurate enough that we can’t see it even if it’s there, then not seeing it doesn’t mean anything, one way or the other.

Conservation of Momentum

Since this is a part of the story of where physics was in 1895, I’ll put it out, here, that as of that time, no exception was known. Every time we could measure things, momentum was conserved. It was considered a solid part of physics.

Because a vector consists of two components, and the addition rules keep the two components separately, you could treat the conservation of momentum as if it were two separate laws, conservation of momentum in the x direction, and conservation of momentum in the y direction. No one actually does this, but from a bookkeeping standpoint it’s definitely twice as much time with the ledger as conservation of mass is.

And, oh by the way… vectors can be three dimensional, too! It’s then a triple number, and the new axis is the z axis, perpendicular to both the x and y axes. The three edges of a cube that meet at the corner are a good representation of this.

Rockets and Guns

Now for an application. How does a rocket work? It works entirely through momentum. Let’s say the rocket’s mass is a thousand kilograms (one metric ton or “tonne”), including the fuel it has on board. And let’s furthermore imagine that it’s out in space somewhere.

A rocket engine works by shooting matter—burnt rocket fuel, to be specific—out the nozzle at very high velocity.

So if the rocket burns one kilogram of fuel plus oxidizer, and shoots the combustion product out the nozzle at 4000 m/s, what happens?

Let’s do this in one dimension for simplicity. The direction the rocket is pointed is positive. And we’re moving along with it, so it looks stationary to us. The rocket, including the fuel, has a momentum of zero.

The momentum of the rocket fuel after it has been burned is 1kg • -4000m/sec. (Negative because the rocket is blowing the exhaust out behind it, the nose points in the positive direction, the nozzle points in the negative direction.

If momentum is conserved, the rocket must now also have a momentumm, this time of +4000 kg•m/s. The rocket has a mass of 1000 kg, so that works out to the rocket now moving at 4 m/s in the forward direction.

So if we want another 4 m/s, burn another kilogram of fuel and oxidizer, right?

Good logic, but there’s a complication here. Because the rocket burned 1 kg of its own mass to get to this point, and now it masses 999 kg, So another kilogram of fuel, adding 2000 kg•m/s to the rocket’s momentum, will actually add slighly more than 4 m/s, precisely 4000/999 m/s, in fact.

For that matter, if you think about it, the mass of the rocket was declining while we did that first burn, so we must have gained a tiny bit more than 4 m/s even the first time around.

That’s quite true, actually, and the real formula for how much velocity a rocket gains by burning some amount of fuel is a bit more complex. But the takeaway is that even in following the other formula, the rocket and its burnt fuel are abiding by the conservation of momentum; in fact it relies on it to operate.

(If you’ve ever heard astronauts, or NASA types, talking about “delta vee”, that’s a reference to the total change in velocity given how much fuel is left, or alternatively, they’re talking about the total change in velocity for a specific maneuver, because that will be equivalent to a cost in fuel for that rocket, with its current mass.)

How about firing a gun? It’s sort of the flip side of a rocket. With a rocket the goal is to make the big thing move, and flinging the fuel out as fast as possible is a means to that end. With a gun, the goal is to make the little thing (the bullet) move, and the gun kicking in the opposite direction is the price paid.

Why does the muzzle flip up on a handgun? Shouldn’t it go straight back, instead of up? It would, except that the line of the barrel does not go through the gun’s center of mass, so there’s a bit of torque there, that causes the whole gun to rotate. If you grip it solidly enough, it kicks your arm up too. Tense up your arm and the entire weight of your body resists the torque and you don’t move much. (Torque, by the way, is another concept that beginning physics studies… )

These particular scenarios are also vivid illustrations of Newton’s third law: for every action, there is an equal but opposite reaction.

This is actually just another way of stating the conservation of momentum. And the first person to put forward the observation that momentum seemed to be conserved was John Wallis in 1671. Newton put forward his three laws in 1687.

Vector Fun

OK, here’s another application of stuff we’ve learned today. You have two identical cannonballs. You drop one. (Hopefully not on your foot.) At the same instant, the other is fired out of a cannon, perfectly horizontally. (Hopefully at a deserving target.) Oh, and you do your drop at the same height as the cannon’s muzzle.

If you’re on perfectly flat ground, which cannonball hits the ground first?

They hit at the same time.

Look at it from a vector standpoint. X is the direction the cannon fires. Y is straight up.

The dropped cannonball starts the experiment with v=[0,0]m/s. The fired cannonball, on the other hand, starts out with v=[200, 0]m/s. I just made that x number up; it doesn’t matter what it is as you’ll see in a moment. (Well, you’ll see it if if I did my job right, today.)

The force of gravity imparts an acceleration of –9.8 m/s² in the y direction, i.e., straight down.

This acceleration can only affect the y component of the velocity vectors, since it’s purely in that direction. And in the y direction, both cannonballs are stationary and in the same place when the experiment starts.

Thus, they both have the same fall, and they will both hit at the same time. It doesn’t matter how fast one of them is moving sideways! And in fact they don’t even need to be the same weight.

I’ve seen demos of this principle done where steel ball bearings are used, in a special little gizmo that drops one the same time a spring shoots the other one out horizontally. You only hear one clack as both balls hit at the same time.

Can’t Get the Drift

Last time around, I highlighted what was, in 1895, a standing mystery. Gravitation seemed to work, except they couldn’t figure out what was going on with Mercury’s orbit about the Sun. A similar problem with Uranus had led to the discovery of Neptune, so it seemed as if there must be some planet closer to the Sun than Mercury, lost in the Sun’s glare, perturbing its orbit. Despite the best efforts of astronomers, that planet (already pre-named Vulcan) had never been found.

This time I’m going to highlight a different little issue.

I mentioned before that velocities were additive, right? A ball thrown by a pitcher on board a moving train ends up moving, relative to the outside observer, faster or slower than the pitcher threw it, by the speed of the train, depending on the direction of the throw.

Can we do this with other things? Sound, for instance, travels at a specific speed (one which varies depending on temperature, humidity, pressure, whether His Fraudulency is on or off his meds, and a host of other factors, but still, a speed that will remain constant until one of these factors changes). Trains have a nice source of sound on them, the whistle (or today the horn). So how fast is the sound travelling in front of the train, and how fast is it travelling behind the train? Measurements from the ground show that they are travelling at the same speed, not different speeds. (They also show that in front of the train the pitch is higher, but that effect is a different rabbit hole. Some other time, perhaps. No, some other time, definitely.) What’s going on here?

It turns out that sound is a wave that travels through a medium, air. It’s going to move at a certain speed relative to the air.

The train is moving, the air is not (unless it’s Wyoming). Thus the sound wave travels the same speed in all direction from the train’s whistle (horn), as heard from someone on the ground on a breezeless day. If some bored passenger on the train were to measure the speed of sound (assuming they’d let him climb around on top of the train in the first place), he’d hear the sound move slower, relative to the train, when measured from in front of the whistle, at a normal speed to the side of the whistle, and faster behind the whistle. He could even figure out how fast the train was going by taking the difference between his “in back of” reading and his “in front of” reading and dividing by two. If he were really ignorant of how trains move, he could even prove it wasn’t moving sideways, but rather forward, this way.

Looking at light, we had originally thought it was instantaneous, it was so doggone fast. But then… well, remember Jupiter’s moons from last time? We could predict their motions once we knew Newton’s law of gravitation, actually we could do so from Kepler’s laws of planetary motion, known earlier. (We didn’t even really need to know the mass or distance to Jupiter to be able to do that.) Well, there was one little anomaly. We could predict the motions all right, but the motions were about eight minutes and twenty seconds early when we were closest to Jupiter, and 8 minutes and 20 seconds late when we were farthest from Jupiter.

A little thought and someone realized, that the difference was due to the speed of light not being infinite. What we see now going on around Jupiter actually happened at some time in the past, when the light left Jupiter. It then took some amount of time for the light to get here.

The 8 minutes and 20 seconds, really in total a 16 minutes and 40 seconds difference, reflect the amount of time it took light to span the entire width of the earth’s orbit about the Sun, because it has to cover that much additional distance when we are farther away, versus closer, to Jupiter. (This works out to about a 1,000 seconds, by the way, a neat coincidence.)

We didn’t know how big the earth’s orbit was, and wouldn’t until the 1760s. Before that we just knew however big it was, light took a 1,000 seconds to cross it, you could even call it a distance of 1,000 light seconds. But once we discovered that the Earth’s orbital diameter is roughly 300,000,000 kilometers, we now knew light moved at about 300,000 kilometers per second (186,000 miles per second). This was another product of all that work measuring the solar system that I totally forgot about when writing that article (which is OK, because it fits better here anyway).

Light was, and is, believed to be a wave. So, presumably it goes through a medium, just like sound does. But it must be an otherwise intangible medium, or planet earth would be suffering drag plowing through it. Only light could “feel” that medium. We knew it had to be there, and so we gave it a name: It was the ether.

We might not be able to feel the ether, but we sure as heck ought to be able to measure the Earth’s velocity through it, the same way as the man on the train: by measuring the speed of light in different directions here on Earth.

Measuring the speed of light in a laboratory was difficult to do accurately in the mid 1800s, but we could be much more precise by comparing two different beams of light in two different directions, and seeing what the difference in their speed is.

Michelson and Morley tried this in 1887. They found no difference in the speed of light no matter which way they measured.

Well, it’s possible that at that point in our orbit, we just happened to be stationary with respect to the ether. But that couldn’t be true a couple of months later, because the earth would at the very least be orbiting in a different direction, so they kept trying.

Others have tried too, with much better equipment.

No difference. Ever. No one has ever “got the drift.”

What’s going on here? Well, that, like Vulcan, was a mystery as 1895 dawned.